Definisi Matriks dan Contoh nya

Definisi matrik
Definisi wikipedia "Dalam matematika, matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. 
 Matriks adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.


  Contoh Matriks
1. Matrik berordo 2x2 (matrik yang mempunyai 2 baris dan 2 kolom)



 

2. Matriks berorodo 2x3 (matriks yang mempunyai 2 baris dan 2 kolom) 
      contoh nya 

\begin{bmatrix}1 & 9 & -13 \\20 & 5 & -6 \end{bmatrix}.

3. Matriks berorodo 3x3 (matriks yang mempunyai 2 baris dan 2 kolom) 
      contoh nya














Perkalian Skalar
Matriks dapat dikalikan dengan sebuah skalar.
\lambda\cdot A := (\lambda\cdot a_{ij})_{i=1, \ldots , m; \ j=1, \ldots , n}
Contoh perhitungan :
5 \cdot \begin{pmatrix} 1 & -3 & 2 \\ 1 & 2 & 7 \end{pmatrix} = \begin{pmatrix} 5 \cdot 1 & 5 \cdot (-3) & 5 \cdot 2 \\ 5 \cdot 1 & 5 \cdot 2 & 5 \cdot 7 \end{pmatrix} = \begin{pmatrix} 5 & -15 & 10 \\ 5 & 10 & 35 \end{pmatrix}

Perkalian matriks

Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama.


c_{ij}=\sum_{k=1}^m a_{ik}\cdot b_{kj}
Contoh perhitungan :
\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \cdot \begin{pmatrix} 6 & -1 \\ 3 & 2 \\ 0 & -3 \end{pmatrix} = \begin{pmatrix} 1 \cdot 6 + 2 \cdot 3 + 3 \cdot 0 & 1 \cdot (-1) + 2 \cdot 2 + 3 \cdot (-3) \\ 4 \cdot 6 + 5 \cdot 3 + 6 \cdot 0 & 4 \cdot (-1) + 5 \cdot 2 + 6 \cdot (-3) \\ \end{pmatrix} = \begin{pmatrix} 12 & -6 \\ 39 & -12 \end{pmatrix}

Jenis-jenis Matriks

Jenis-jenis matriks dapat dibagi berdasarkan ordo dan elemen / unsur dari matriks tersebut.

Berdasarkan ordo Matriks dapat di bagi menjadi beberapa jenis yaitu :
  • Matriks Bujursangkar adalah matriks yang memiliki ordo n x n atau banyaknya baris sama dengan banyaknya  kolom yang terdapat dalam mtriks tersebut. Matriks ini disebut juga dengan matriks persegi berordo n.
          Contoh : 


  • Matriks Baris adalah Matriks Baris adalah matriks yang terdiri dari satu baris
          Contoh :    A =  ( 2  1  3  -7 )
  • Matriks Kolom adalah  Matriks Kolom adalah matriks yang terdiri dari satu kolom.
          Contoh :   
                            
  • Matriks Tegak  adalah  suatu matriks yang banyaknya baris lebih dari banyaknya kolom.
          Contah :
  • Matriks datar adalah Matriks  yang banyaknya baris kurang dari banyaknya kolom.
       Contoh :



Berdasarkan elemen-elemen penyusunnya matriks  dapat di bagi menjadi beberapa jenis yaitu :
  • Matriks Nol adalah Suatu matriks   yang setiap unsurnya 0 berordo  m x n, ditulis dengan huruf  O. 
        contoh :
  • Matriks Diagonal adalah  suatu matriks bujur sangkar yang  semua unsurnya , kecuali unsur-unsur pada diagonal utama adalah nol.
       Contah :  

1 komentar:

  1. Vonny Ramadhani3 Oktober 2020 pukul 03.07

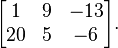
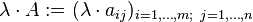
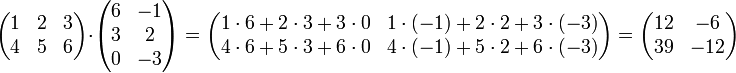
    thanks kak info nya, semangat ya kak buat artikel-artikel yang bermanfaat lainnya.
    Perkenalkan kak nama saya Vony Ramadhani TP Dari ISB Atma Luhur

    BalasHapus

Langganan: Postingan (Atom)